Understanding Count-Min Sketch: A Probabilistic Data Stucture
In the world of big data, where massive amount of information flow like raging rivers, it's crucial to have efficient techniques for summarising and approximating data streams. Count-Min Sketch, a probabilistic data structure that allows us to estimate the frequencies of elements in a data stream with remarkable accuracy and space efficiency.

Have you ever wondered how Youtube views are counted, or how instagram or Facebook likes are count. Keeping track of the exact count of every view or like would require an enormous amount of memory, quickly becoming a bottleneck in your system. This is where the Count-Min Sketch comes to the rescue, providing a clever way to estimate these frequencies with a high degree of accuracy while using a fraction of the memory.
Count-Min Sketch was developed by Graham Cormode and S. Muthukrishnan in 2005; this data structure offers an efficient and space-saving solution for situations where exact counts are not necessary but speed and memory efficiency are paramount.
What is Count-Min Sketch?
Count-Min Sketch is a probabilistic data structure that provides approximate counts of elements in a stream. It's particularly useful for applications where you need to process massive amounts of data quickly and with limited memory. Examples include network traffic monitoring, database queries, and natural language processing tasks.
How does it work?
At its core, the Count-Min Sketch is a two-dimensional array with a depth of d and a width of w. Each row of the array represents a different hash function, and each column corresponds to a distinct element in the data stream. The algorithm works by hashing the elements and incrementing the corresponding counters in the array.
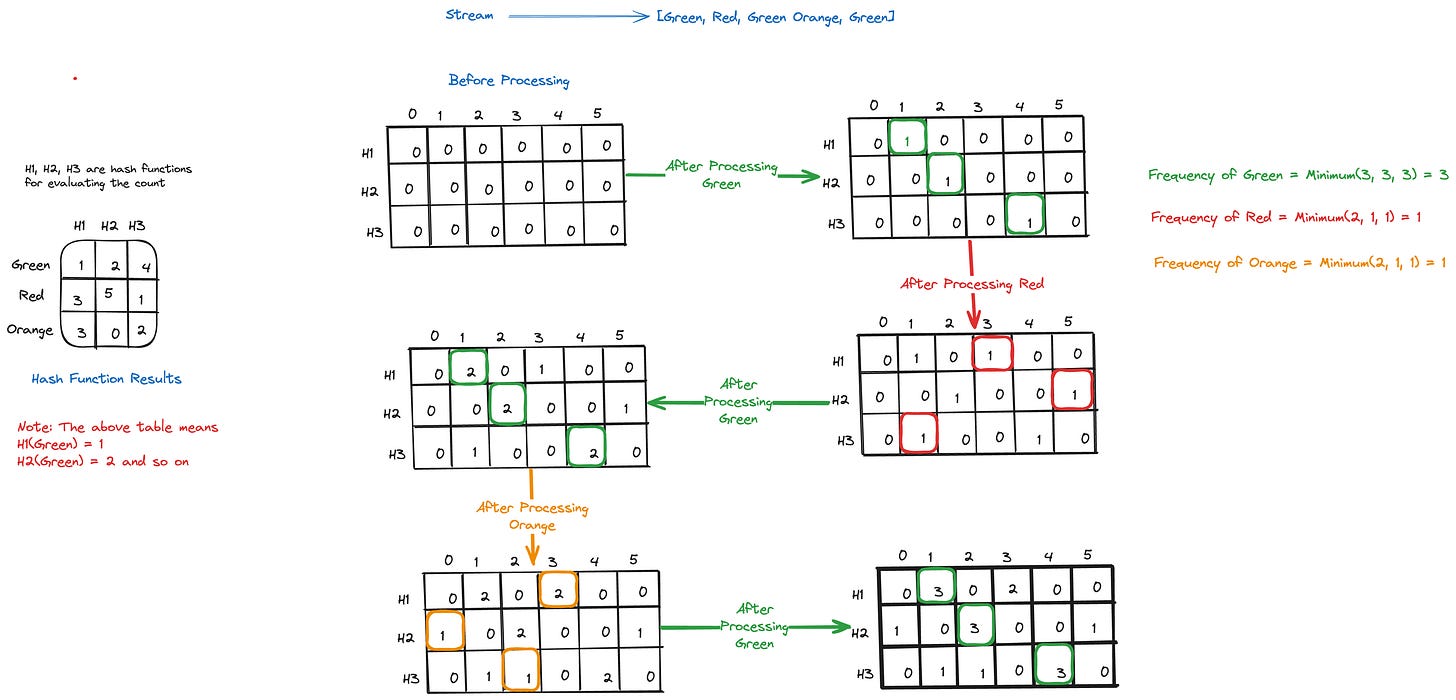
To understand how this works, let's consider a simple example. Suppose we have a data stream of colours, and we want to estimate the frequency of each colour. We can initialise a Count-Min Sketch with a depth of d=3 and a width of w=5, giving us the following array:
As each colour is being processed, we update our count-min sketch array with the corresponding hash result for the various hash functions. In our case, we have three hash functions and we fill in the result in the count-min sketch array for each of the hash function for a particular colour. From the example above, we can see that there is a hash collision where the H1 resulted in column 3 for both Red and Orange. Count-Min sketch minimises the impact of these hash collisions by taking the minimum count value of all rows (i.e hash functions) for the corresponding columns, as the probability of collisions happening in all hash function is low.
By taking the minimum value across rows, the Count-Min Sketch provides a conservative estimate of the frequency, minimising the impact of collisions while still offering a reasonable approximation.
One of the major advantages of the Count-Min Sketch is its space efficiency. The total memory required for the data structure is O(d * w), where d is the depth (number of rows) and w is the width (number of columns). By carefully tuning these parameters, you can achieve a desired balance between accuracy and memory usage.
In terms of time complexity, the Count-Min Sketch operates in O(d) for both insertions and queries, making it highly efficient for real-time data processing applications, where d is the number of hash functions.
Choosing the width and number of Hash functions
Choosing the number of hash functions (𝑑) and the width of the hash table (𝑤) in a Count-Min Sketch involves balancing accuracy, memory usage, and the probability of errors.
The width of the hash table, 𝑤, determines the range of possible hash values and thus influences the accuracy of the frequency estimates.
Error Bound (𝜖): The width 𝑤 is inversely proportional to the error bound 𝜖. The error bound 𝜖 is the maximum amount by which the Count-Min Sketch can overestimate the frequency of any element.
\(w = \lceil \frac{e}{\epsilon} \rceil \)
The number of hash functions, 𝑑, determines the number of times an element is hashed and thus influences the probability of overestimation.
Probability of Error (𝛿): The number of hash functions 𝑑 is logarithmically related to the probability 𝛿 that any given estimate exceeds the true count by more than the error bound 𝜖.
\(d = \lceil \ln \frac{1}{\delta} \rceil \)
Example Calculation
Suppose you want an error bound of 𝜖=0.01 (1%) and a probability of error δ=0.01 (1%).
Calculate 𝑤
\(w = \lceil \frac{e}{\epsilon} \rceil = \lceil \frac{2.718}{0.01} \rceil = \lceil 271.8 \rceil = 272 \)Calculate 𝑑:
\(d = \lceil \ln \frac{1}{\delta} \rceil = \lceil \ln \frac{1}{0.01} \rceil = \lceil \ln 100 \rceil = \lceil 4.605 \rceil = 5 \)
Practical Application of Count-Min Sketch
The Count-Min Sketch has found widespread applications in various domains, such as:
Data Stream Summarisation: As demonstrated in our streaming service example, the Count-Min Sketch is particularly useful for estimating frequencies in massive data streams, enabling real-time analysis and decision-making.
Network Traffic Monitoring: Network administrators can use the Count-Min Sketch to track the frequency of IP addresses, URLs, or other network data, enabling efficient detection of anomalies or security threats.
Database Query Optimisation: In database systems, the Count-Min Sketch can be used to estimate the selectivity of queries, helping the query optimiser make more informed decisions about query execution plans.
Bloom Filters: The Count-Min Sketch can be used in conjunction with Bloom Filters, another probabilistic data structure, to estimate the number of distinct elements in a set, enabling efficient cache management and data deduplication.
Conclusion
Count-Min Sketch is a remarkable tool for handling large-scale data streams with efficiency and ease. Its ability to provide approximate counts with minimal memory usage makes it ideal for many real-world applications. As data continues to grow exponentially, understanding and utilising data structures like Count-Min Sketch will be increasingly important for data professionals.
We hope you found this deep dive into the Count-Min Sketch algorithm both engaging and informative. Stay tuned for more insights and explorations in the next issue of Byte Beat.


Thank you for the learning opportunity 🙏🏾